背景
在電腦科學中,我們常將問題分類到各種不同的類別裡(例如:NP問題、無法解決(Unsolvable)的問題、遞迴(Recursive)的問題)。在這個問題裡,你將分析一個演算法的特性,而這個演算法對於所有可能的輸入來說,並不知道其分類為何。
問題
考慮到下面的演算法:
- 輸入n
- 印出n
- 當n等於1時停止
- 如果n是奇數,則
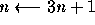
- 其餘的狀況,則
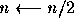
- 回到第二步驟
給予一個輸入22,則會印出下列的數列: 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
上面這個演算法目前被推測認為在給予任何整數輸入值時皆可以停下來(也就是說最後都能夠輸出1)。儘管這個演算法還蠻簡單的,但卻無法確定這個推測是否是正確的;然而可以確定的是,在輸入值n介於0到1,000,000之間時,這個推測是正確的(實際上,還有比0到1,000,000更多的輸入值也是可以讓演算法停下來)。
給予一個輸入n,我們可以去算出總共會有幾個數字會被印出(包含1),而這個總數就被稱作n的循環長度(cycle-length of n)。在上面的範例中,22的循環長度為16。
輸入
輸入會有一系列好幾對的整數i和j,每一對整數i和j會佔一行。所有整數會小於1,000,000並且大於0。
你應該運算每一個包含整數i和j與介於其之間的任意整數中可以造成的最大的循環長度是多少。
你可以假設沒有任何運算超過32位元整數。
輸出
對於每一對的整數i和j,你應該輸出i和j以及包含整數i和j與介於其之間的任意整數中最大的循環長度的值。對於每行輸入所要輸出的這三個數字應該放在同一行,並在數字中間至少用一個空白隔開。整數i和j必須依照在輸入之中的順序輸出,並且後面還要跟著最大的循環長度(在同一行)。
範例輸入
1 10
100 200
201 210
900 1000
範例輸出
1 10 20
100 200 125
201 210 89
900 1000 174
翻譯:灆洢。若翻譯有任何錯誤,歡迎底下留言告知,感謝!

